Ternary Composition Variation
of Vinyl Terpolymers

Composition As a Function of Blend Conversion

Many commercial polymers are produced by copolymerization of two or more monomers. The combination of several monomers allows for a broad variation and optimization of the polymer properties such as tensile strength, elasticity, transparency, solvent resistance, and dimensional stability. Furthermore, multicomponent polymers with tailored monomer sequences such as alternating, gradient or block arrangements possess unique properties that are very different from those of neat polymers or polymers with random monomer sequences. For this reason, the prediction of the (instantaneous) polymer composition as a function of feed composition is of great value to the polymer chemist.

Quite often three or more monomers are simultaneously polymerized. The resulting copolymers are called terpolymers, quaterpolymers, etc. The kinetics of such a polymerization was first investigated by Alfred and Goldfinger in 1944.^1-3 They showed that the kinetic behavior of a terpolymerization is governed by nine different propagation reactions. These reactions together with the corresponding propagation rate equations (rate of monomer consumption), R_ij, are shown below:

A· + A → A·      R_AA = k_AA [ A·] [ A ]
A· + B → B·      R_AB = k_AB [ A·] [ B ]
A· + C → C·      R_AC = k_AC [ A·] [ C ]

B· + A → A·      R_BA = k_BA [ B·] [ A ]
B· + B → B·      R_BB = k_BB [ B·] [ B ]
B· + C → C·      R_BC = k_BC [ B·] [ C ]

C· + A → A·      R_CA = k_CA [ C·] [ A ]
C· + B → B·      R_CB = k_CB [ C·] [ B ]
C· + C → C·      R_CC = k_CC [ C·] [ C ]

where A·, B· and C· represent chain radicals of type A, B and C; [A], [B], and [C] are the corresponding monomer concentrations; and k_ij are the rate constants of the nine different types of free radical polymerization reactions. It is assumed that radicals ending in A - A·, B - A· and C - A· have equal reactivities towards any given monomer.

The rates of disappearance of the three monomers of a terpolymerization can be written in the following form

d[A]/dt = R_AA + R_BA + R_CA
d[B]/dt = R_AB + R_BB + R_CB
d[C]/dt = R_AC + R_BC + R_CC

If the polymer chains are sufficiently long, both initiation and termination are exceedingly rare events. Furthermore, at a steady state, the generation and elimination of radicals are equal, and monomers are only consumed in the propagation reaction. Then we have

R_AB + R_AC = R_BA + R_CA
R_BA + R_BC = R_AB + R_CB
R_CA + R_CB = R_AC + R_BC

By combining the two sets of equations and using the appropriate rate equations, Alfrey and Goldfinger (1944) found following expression for the instantaneous ratio of monomers in the terpolymer as a function of feed composition:

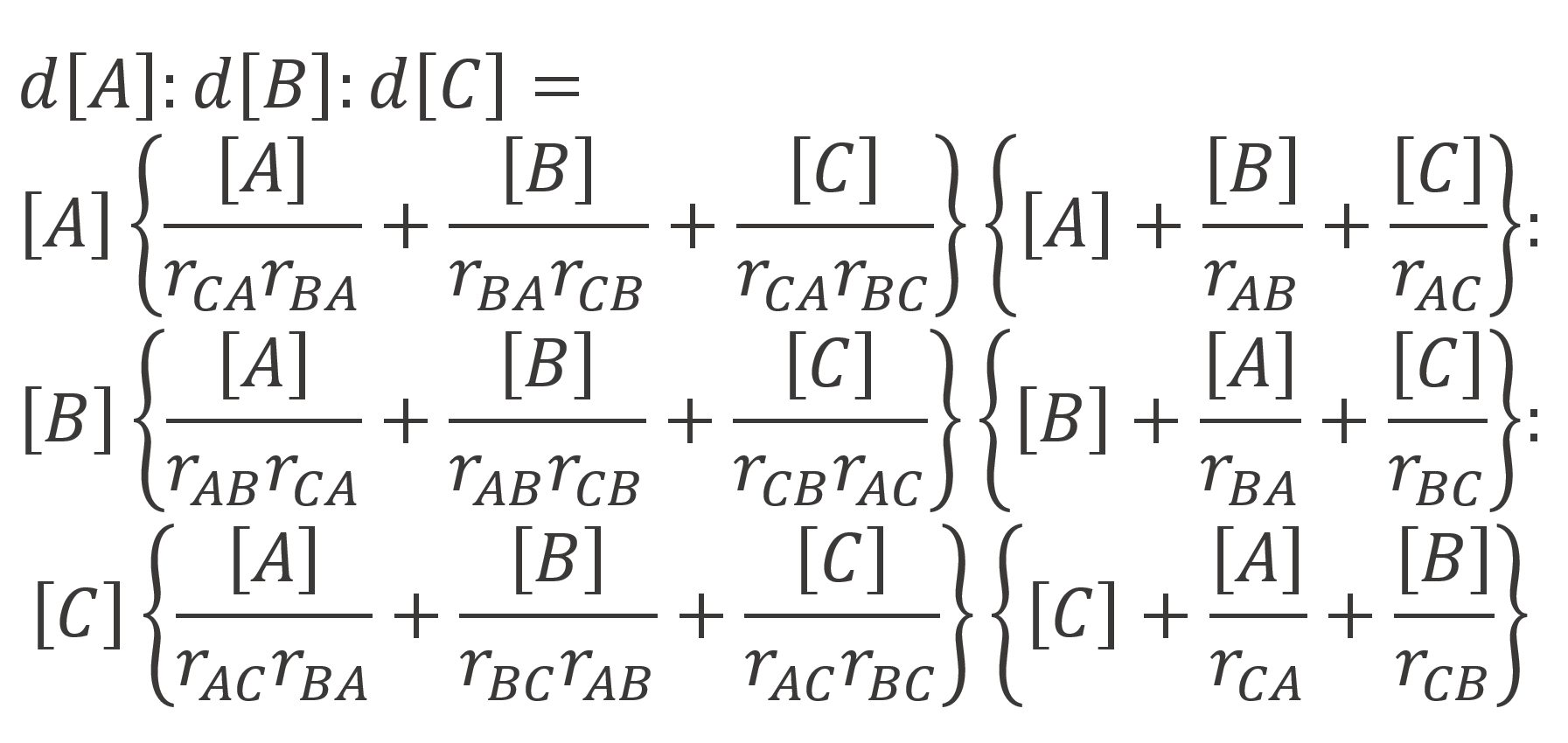
where r_ij are the (binary) monomer reactivity ratios defined by r_ij = k_ii / k_ij
As has been shown by Hocking and others, the Alfrey-Goldfinger equation is in good agreement with experimental results.⁴

A somewhat simpler expression that yields similar compositions for terpolymers was developed by Valvassori and Sartori (1967) who used following simpler steady state equations:⁵

R_AB = R_BA
R_BC = R_CB
R_CA = R_AC

By combining these steady state relations with the rate equations derived by Alfrey and Goldfinger, Valvassori and Sartori obtained:

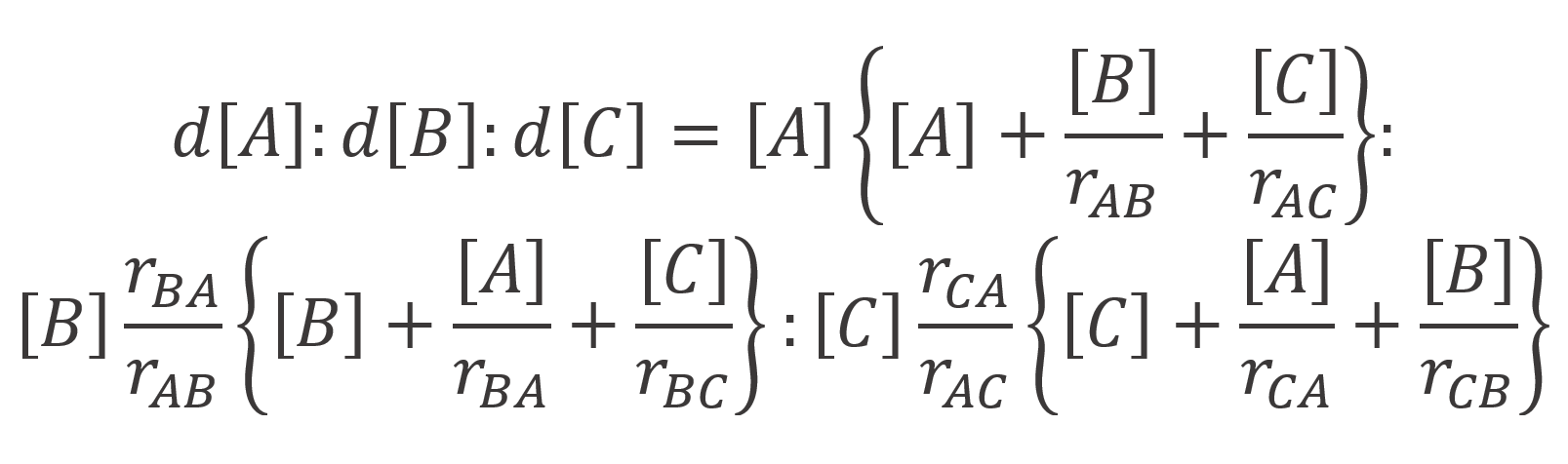
Recently, Kazemi et al.⁶ derived new terpolymer composition equations that eliminate symmetry issues and other errors. This significantly improved the reliability of the estimated ternary reactivity ratios r_ij.⁷ Their expressions are equivalent to the Mayo-Lewis equation, modified for three-component systems:^6,8

They also derived expressions for the binary rartios of the instantaneous terpolymer compositions (F_i/F_j) as a function of unreacted monomer mole fractions (f_i):^6-8

The Alfrey and Goldfinger (A-G) model provides only ratios of the instantaneous mole fractions, that is the monomer mole fractions in the terpolymer are not presented explicitly. However, the measured compositions are typically single mole fractions and not ratios. According to Kazemi et al., this will have a severe impact on parameter estimates. To overcome this problem, Kazemi et al. recast the A-G model so that each terpolymer mole fraction is presented as a single response:^6-10

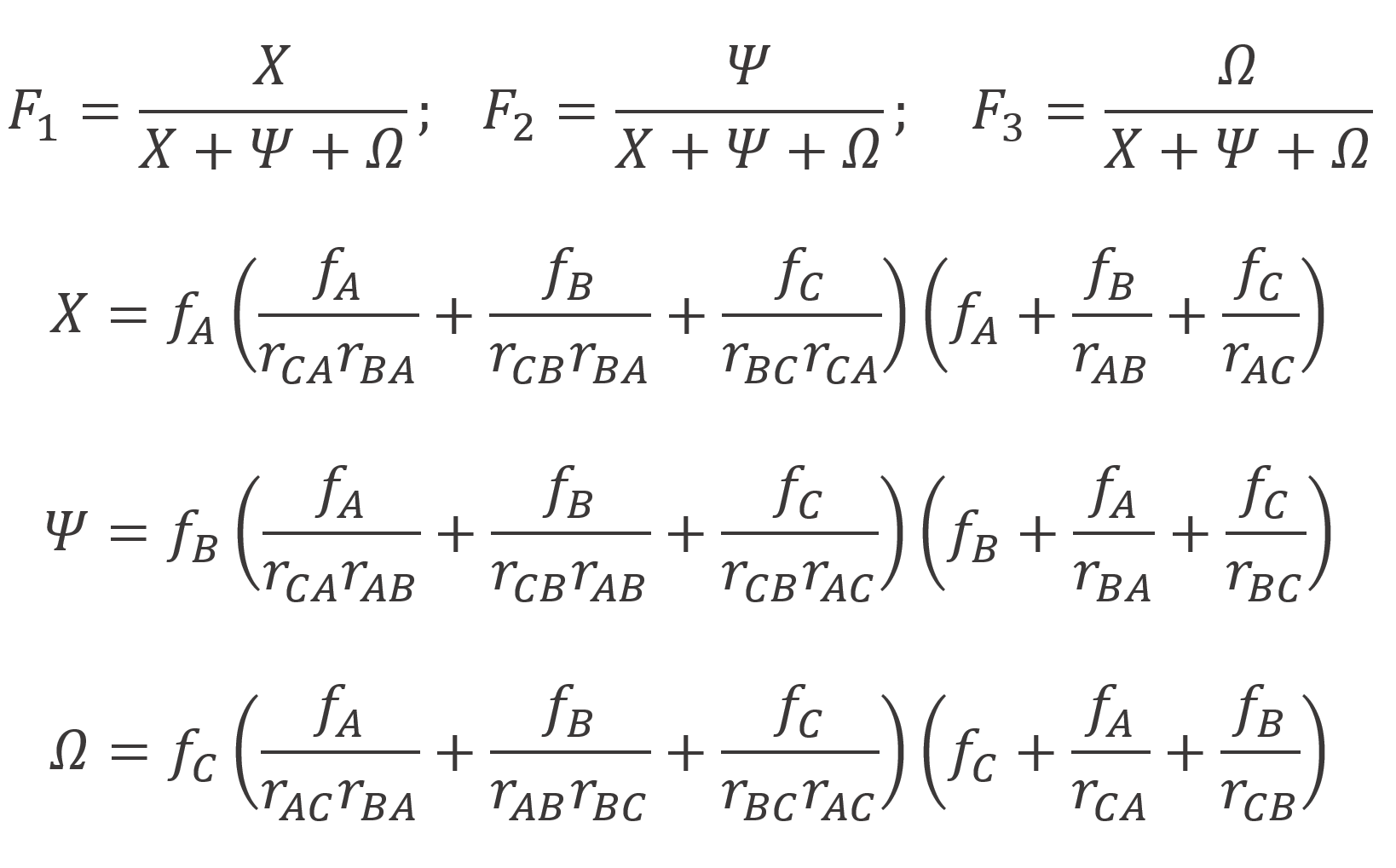
In order to calculate the instantaneous terpolymer compositions (F_i) as a function of feed composition (f_i), six reactivity ratios r_ij are needed. Unfortunately, for many ternary systems, these parameters are unknown. In these cases, it is tempting to use binary reactivity ratios, which, in fact, are quite often employed for ternary systems. However, according to Kazemi et al.^6,9, they are often poor approximations of the true reactivity ratios of ternary systems and thus may lead to large errors in the composition prediction. Instead, an error-in-variables-model should be employed to estimate reactivity ratios.^10,11

The composition of the feed and terpolymer are typically presented in the form of a triangular plot. The direction of compositional drift in the terpolymer is often depicted by arrows.

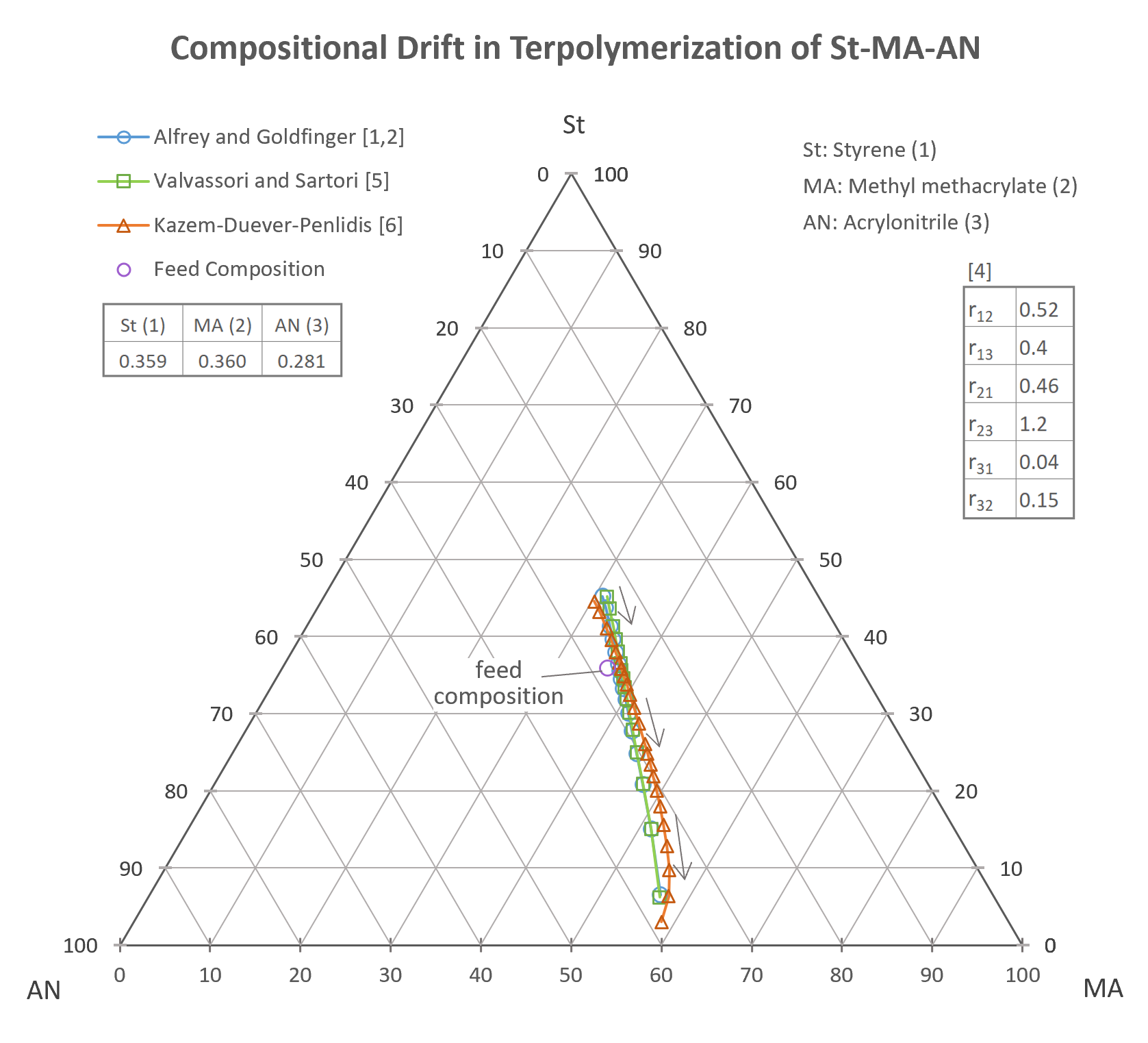
The triangular plot above shows the calculated ternary composition variation for the system styrene(1) - methyl methacrylate(2) – acrylonitrile(3). The ternary reactivity ratios have been taken from [4] and the composition curves have been calculated with the three models discussed above. The compositions predicted with the A-G and V-S model are almost identical whereas the model developed by Kazemi et al. gives slightly different terpolymer compositions.

Note, the multicomponent composition equations presented above are generally valid only when all the monomer reactivity ratios have finite values; that is, when one or more of the monomers is not capable of homopolymerization the expressions become indeterminate. For these and other special cases, several modified expressions based on both conventional and simplified models have been derived.

References & Further Readings:

1. T. Alfrey & G. Goldfinger, J. Chem. Phys. 12, 205 (1944)
2. T. Alfrey & G. Goldfinger, J. Chem. Phys., 12, 322 (1944)
3. T. Alfrey & G. Goldfinger, J. Chem. Phys., 14 115 (1946)
4. M.B. Hocking & K. A. Klimchuk, J. Poly. Sci.: Part A: Poly. Chem. 34, 2481-2497 (1996)
5. A. Valvassori & G. Sartori, Adv. Polym. Sci., 5, 28 (1967)
6. N. Kazemi, T.A. Duever & A. Penlidis, AIChE Journal, 60, 1752-1766 (2014)
7. A.J. Scott & A. Penlidis, Europ. Poly. J. 105, 442-450 (2018)
8. N. Kazemi, Thesis: Reactivity Ratio Estimation Aspects in Multicomponent Polymerizations, University of Waterloo, Ontario, Canada 2010
9. A.J. Scott, N. Kazemi & A. Penlidis, Process, 5(1), 9 (2017)
10. N. Kazemi, T.A. Duever & A. Penlidis, Comput. Chem. Eng., 48, 200-208 (2013)
11. A.J. Scott and A. Penlidis, Processes, 6(1), 8 (2018)
12. R. Slocombe, J. Poly. Sci., vol. XXVI, pp. 9-22 (1957)
13. A.J. Scott, V.A. Gabriel, M.A. Dube & A. Penlidis, Process, 7(7), 444 (2019)
14. A.K. Srivastava & M. Kamal et al., J. Poly. Res. 9, 213-220 (2002)
15. Masoud Soroush, Computational Methods for Polymers, Basel, Switzerland 2020

April 2, 2022